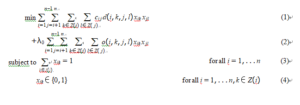AC Power Converter Circuitry Board Cloning

AC Power Converter Circuitry Board Cloning can help engineer to extract the Layout diagram out from physical PC Board sample, but the component placement issue still need to carry out the analysis.

The objective function is composed of two terms: (1) is an approximation of the total wire length computed in the following way: ci j ≥ 0 denotes the affinity coefficients between the components i and j and can be calculated by ci j = ∑t∈T α 1 if t is a net connecting i and j, and zero otherwise. T is the set of all nets, αt the cardinality of a net t ∈ T . d(i, k, j, l) defines the shortest Manhattan distance between the components i and j when assigned to the grid cells k and l.

The second term  (2) of the objective function evaluates the number of overlaps.  The coefficients  o(i, k, j, l) defined for i ∈ {1, . . . , n}, j ∈ {1, . . . , n}, k ∈ Z(i) and l ∈ Z( j) counts the number of grid cells that are shared by components i and j when assigned to grid cells k and l. Since a feasible placement has to be free of overlaps, the second term of the objective function is scaled with a large penalty factor λ₀. Equations (3) ensure that each component is assigned to exactly one grid cell.

This quadratic optimization formulation allows the following extension: when some components are allowed to be rotated 90◦, four different realizations exist to place each of these components. In this case, binary variables xa are defined for a component i in grid cell k ∈ Z(i) and for realization a ∈ A(i), such that ik is equal to one if and only if the component i is assigned to the feasible grid cell k in realization a. The extended quadratic placement problem is the following:

Where d(i, k, a₁, j, l, a₂) denotes the shortest Manhattan distance between components i and j when placed on grid cells k and l in realization a₁ and a₂, and oj(i, k, a₁, j, l, a₂) counts the number of overlapping components i and j when placed on grid cells k and l in realization a₁ and a₂. The quadratic model for component placement described above belongs to the class of NP-hard problems. In Weismantel (1992), a decomposition approach is applied to the placement problem.