DC Power Converter PCB Board Cloning
DC Power Converter PCB Board Cloning
So called analytical placement is an approach widely used in VLSI design, which can also be applied to layout diagram component placement of DC Power Converter PCB Board Cloning. An advantage of analytical placement over partitioning-based methods is the global view of the problem. In recursive minimum cut placement, minimizing the number of wires crossing a cut in the first step may lead to poor results in the succeeding steps. We present two classes of global analytical placement approaches: quadratic or linear assignment and quadratic placement.
The quadratic assignment approach is based on the following idea: given a number of components and a number of positions on the board surface, we want to assign each component to a position on the board, so that certain physical constraints are satisfied and the total wire length is minimized. This can be formulated as a linear integer optimization problem with either a linear (Akers, 1981) or a quadratic objective function.
The board surface is assumed to be modeled as a grid which decomposes the board into rectangular grid cells with precisely defined dimensions. A component placed on the grid covers a rectangular area consisting of a set of grid cells.
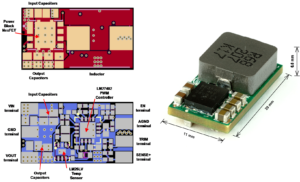
DC Power Converter PCB Board Cloning
The placement problem is to assign the components to disjoint rectangular areas of grid cells such that the total wire length is minimized. A component i is said to be assigned to a grid cell k, if i is placed on the board in such a way, that its lower left corner coincides with grid cell k, and a grid cell k is called feasible for a component i, if i fits on the board when assigned to the grid cell k. Let n be the number of components and m the number of grid cells, then we define Z(i) ⊆ {1, . . . , m} as the set of feasible grid cells for component i.
For each component i ∈ {1, . . . , n} and each feasible grid cell k ∈ Z(i) a binary variable xik is introduced, such that xik is equal to one if and only if component i is assigned to grid cell k. The quadratic assignment model for component placement proposed by Weismantel (1992) is then defined as follows:

